Clustered Level Planarity

Abstract

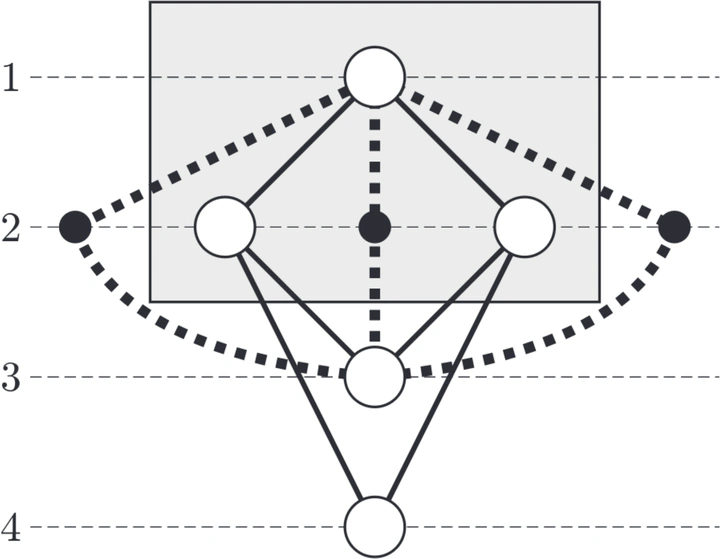
Planarity is an important concept in graph drawing. It is generally accepted that planar drawings are well understandable. Recently, several variations of planarity have been studied for advanced graph concepts such as k-level graphs [16], [15], [13], [14], [11], [12], [10], [6] and clustered graphs [7], [5]. In k-level graphs, the vertices are partitioned into k levels and the vertices of one level are drawn on a horizontal line. In clustered graphs, there is a recursive clustering of the vertices according to a given nesting relation. In this paper we combine the concepts of level planarity and clustering and introduce clustered k-level graphs. For connected clustered level graphs we show that clustered k-level planarity can be tested in O(k|V|) time.