Radial Level Planarity Testing and Embedding in Linear Time

Abstract

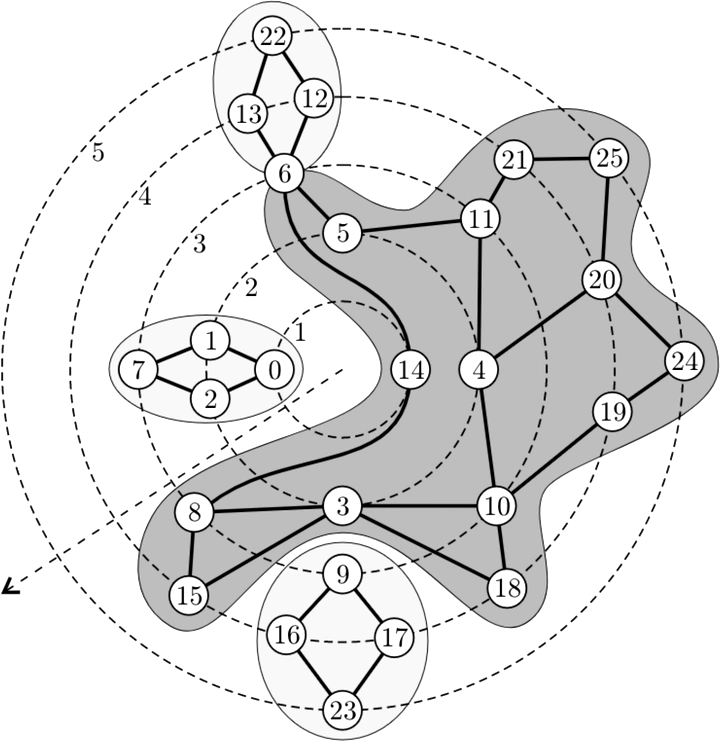
Every planar graph has a concentric representation based on a breadth first search, see [24]. The vertices are placed on concentric circles and the edges are routed as curves without crossings. Here we take the opposite view. A graph with a given partitioning of its vertices onto k concentric circles is k-radial planar, if the edges can be routed monotonic between the circles without crossings. Radial planarity is a generalisation of level planarity, where the vertices are placed on k horizontal lines. We extend the technique for level planarity testing of [13, 14, 16–18, 20] and show that radial planarity is decidable in linear time, and that a radial planar embedding can be computed in linear time.